Ответ
0
(0 оценок)
0
Logicsmile007
4 года назад
Светило науки - 59 ответов - 0 раз оказано помощи
Ответ: 29°
Объяснение:
Сумма углов треугольника равна 180, таким образом:
∠ABC = 180 - 16 - 74 = 90
По свойству высоты, прямая, выходящая из вершины угла образую перпендикуляр с противоположной стороной, тогда:
∠MBC + ∠BCM + ∠CMB = 180 => ∠MBC = 180 - 74 - 90 = 16
По свойствам, медиана делит угол выхода пополам, а потому:
∠KBC = 90 / 2 = 45
Отсюда: ∠KBM = 45 - 16 = 29
Убедимся, что все верно:
∠ABC = ∠ABK + ∠KBM + ∠MBC = 45 + 29 + 16 = 90 - что и требовалось доказать.

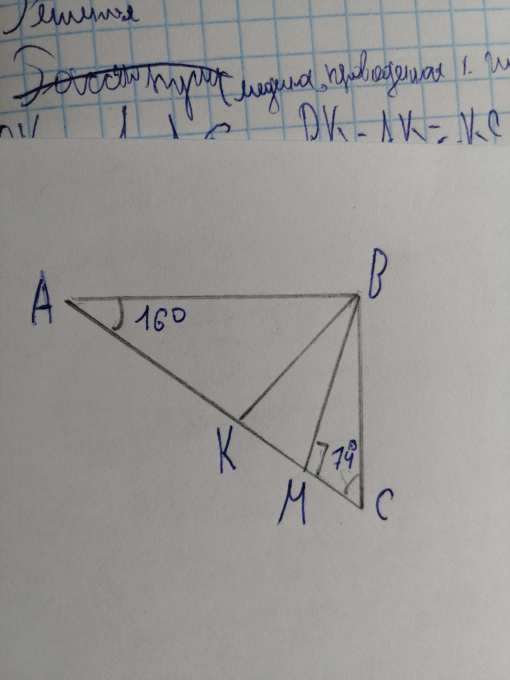
∠АВС=180-(16+74)=90° ⇒ΔАВС -прямоугольный ⇒медиана ВК проходит через середину гипотенузы ⇒ΔАВК-равнобедренный ⇒∠КВА=∠А=16°<br />∠СКВ-внешний для ΔКВА , значит ∠СКВ=16+16=32°<br />ΔМВК-прямоугольный ,∠КВМ=90-∠МКВ=90-32=58°