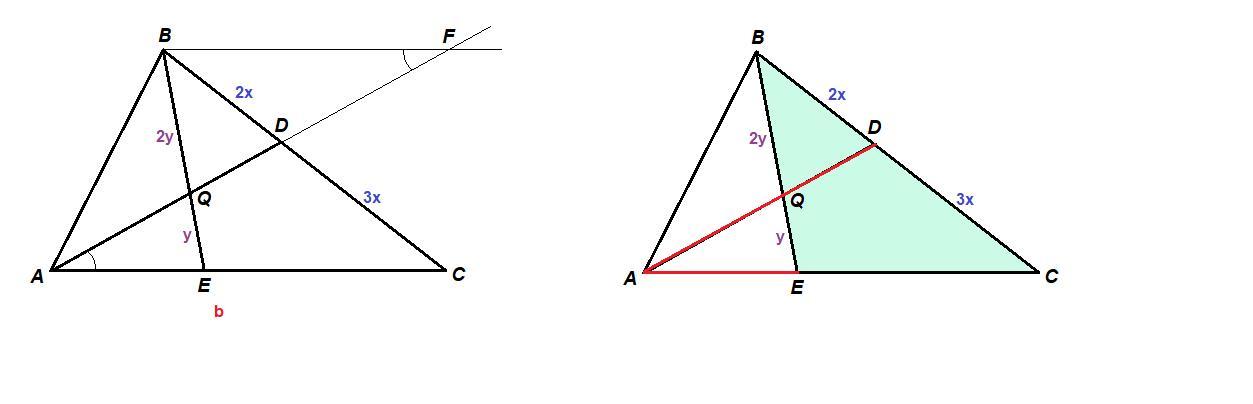
В треугольнике ABC отрезок AD, проведенный из вершины A к стороне BC, делит последнюю в отношении 2:3. Из вершины B к стороне AC проведен отрезок BE, который пересекается с отрезком AD в точке Q так, что BQ = 2QE. Найти, в каком отношении точка E делит сторону AC.
дайте ответ с решением пожалуйста.
дайте ответ с решением пожалуйста.
5
(1 оценка)
2
KuOV
4 года назад
Светило науки - 4906 ответов - 74340 раз оказано помощи
Ответ:
АЕ : ЕС = 1 : 2
Объяснение:
Проведем BF║AС.
ΔBFD ~ ΔCAD по двум углам (∠BFD = ∠CAD как накрест лежащие при пересечении параллельных прямых BF и АС секущей AF, углы при вершине D равны, как вертикальные).
ΔBQF ~ ΔEQA по двум углам (∠BFQ = ∠EAQ как накрест лежащие при пересечении параллельных прямых BF и АС секущей AF, углы при вершине Q равны как вертикальные)
______________________________________________
Задачу можно решить проще, применив теорему Менелая для ΔЕВС:
Отсюда следует, что

Отлично! С задачей с параллелограммом тоже разобрались?
Да, её тоже понял.
Отлично! Будут интересные задачки, выкладывайте. Удачи!
От какой стороны тут размышлять по фалесу?
Строите EF||AD Рассматриваете ADC, RFC и BEF, BQD и всё