Ответ:
a)x⁹=-1,сначало нужно упростить уравнение получим
а затем просто вычисляем и получаем
x=-1
b)(x+1)⁸=-1
Данное уравнение ложное так как,для любого значения х,функция должна быть с показателем степени всегда положительным или 0,то что бы не писать это все запишем как
x∉R
в)(x+1)¹²=0 нам нужно приравнять основание степени к 0
x+1=0
x=-1
г)(2x-1)(x+6)=0 у этого уравнения 2 случая как
2x-1=0
x+6=0 решим оба способа как уравнения
=================
2x-1=0
x=
=================
x+6=0
x=-6
что значит что уравнение имеет 2 решения запишем ответа таким образом
Ответ:x₁=-6 x₂=
Объяснение:
Итак, начнем
а) х^9 = -1
Единица в любой степени останется единицей
Из отрицательного числа в нечетной степени получается отрицательное число
Следовательно х = - 1
б) (х+1)^8 = -1
Быть такого не может, так как выражение в честной степени на выходе всегда будет положительным, как ни крути уравнение
Следовательно, х не существует
в) (х+1)^12 = 0
Если какое-то число возвели в степень и получили ноль, то это число равно нулю. В данном случае х+1 = 0, следовательно, х = - 1
г) (2х-1)(х+6)=0
Многие прекрасно знают, что любое число или выражение, умноженное на ноль, становится в произведении 0
Получается, 2х-1=0 или х+6=0
2х = 1
х=0,5
----------------------
х = - 6
Ответ: - 6; 0,5.
Да, здесь будет два корня, не смущайся. В конце 8 класса будешь щёлкать такие уравнения, как орешки

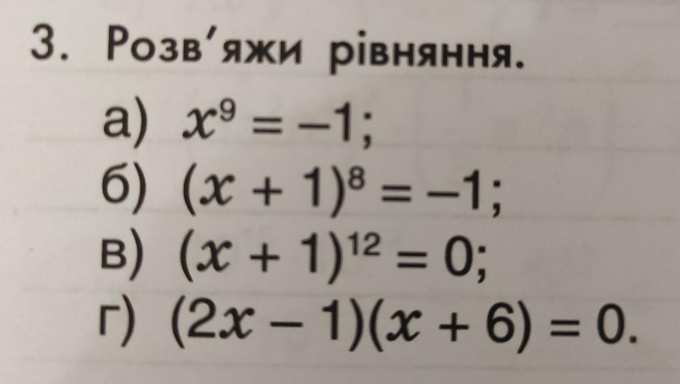
второе, как уже написал. не имеет корней, потому что в результате возведения в четную степень не может получиться отрицательное число
в третьем скобку приравниваешь к нулю, переносишь +1 за знак равно, получается х=-1, вот и ответ
Понял, спасибо большое
да не за что)
(просто скажу что скоро появятся уравнения, где нужно найти все корни, то есть например во 2 уравнении ответ -(степень -8) -1; (степень -8)-1 (степень корня 8, да именно корня (это не корень в 8 степени...))) за это баллы могут лишить за то что не нашел другие корни, хоть они и не могут существовать...